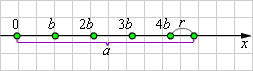
Для натурального числа b всякое целое число a единственным образом представимо в виде a = bq + r, где 0 ≤ r ≤ |b|.

Со времен древних греков известен рисунок, иллюстрирующий доказательство этой теоремы:

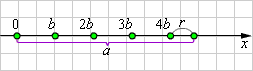
Если натуральное число  p не делится на натуральное число  q, то говорят о делении с остатком. Так, если  p – делимое,  q – делитель и p > q, то p = kq + r, где  r < q, k – частное, r – остаток. Деление без остатка описывается случаем r = 0.

Если положить, например, q = 5 и  r = 1, то получим p = 5k + 1, что представляет собой общую формулу чисел, при делении которых на 5 в остатке получается 1.Деление с остатком

Напомним, что для натурального числа q всякое натуральное число p единственным образом представимо в виде p = kq + r.

Все натуральные числа имеют, по крайней мере, два натуральных делителя: единицу и самого себя. В случае с единицей эти два делителя совпадают. Все остальные натуральные числа (кроме 1) имеют, по крайней мере, два различных натуральных делителя: единицу и самого себя.

Простыми называются натуральные числа, которые не имеют других натуральных различных делителей, кроме единицы и самого себя.

Числа, которые имеют и другие натуральные делители кроме единицы и самого себя, называют составными. 

Число 1 имеет единственный натуральный делитель – самого себя. А значит, согласно данным определениям, оно не является ни простым, ни составным.

Для того, чтобы доказать, что данное натуральное число простое, достаточно установить, что оно не делится ни на одно из чисел от 2 до [N‾‾√] включительно. Если же N делится на одно из таких чисел, то оно составное.

Более удобный способ отбора составных чисел – решето Эратосфена – предложил в III в. до н. э. древнегреческий математик Эратосфен. Предположим, что нам нужно установить, какие из чисел 2, …, N являются простыми. Выпишем их в ряд и вычеркнем каждое второе число из следующих за числом 2 – все они составные, так как кратны числу 2. Первое из оставшихся невычеркнутыми чисел – 3 – является простым. Вычеркнем каждое третье число из следующих за числом 3; следующее из невычеркнутых чисел – 5 – также будет простым. По тому же принципу вычеркнем каждое пятое число из следующих за числом 5 и вообще каждое k-ое из следующих за числом k. Все оставшиеся невычеркнутыми числа будут простыми.

Простых чисел бесконечно много.

Предположим, что ряд простых чисел конечен, и обозначим последнее простое число в этом ряду буквой N. Тогда число x = 1 ċ 2 ċ … ċ (N – 1) ċ N + 1 должно быть составным. Это число при делении на числа 2, 3, …, N – 1, N всякий раз дает в остатке единицу. Таким образом, x не делится без остатка ни на одно из чисел 2, …, N, а простых чисел, бóльших N, по нашему предположению не существует. Но если бы x было составным числом, то оно должно было делиться хотя бы на одно простое число. Мы приходим к противоречию – следовательно, ряд простых чисел бесконечен.

Доказательство этой теоремы принадлежит древнегреческому математику Евклиду и описано в его «Началах».

Приведем список простых чисел в пределах первой сотни: 

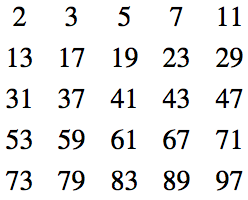
Глядя на эту таблицу, можно убедиться в том, что простые числа распределены в натуральном ряду неравномерно. Существует расположенные рядом простые «числа-близнецы» (2 и 3, 3 и 5, 17 и 19, 41 и 43 и т. д.). С другой стороны, есть бесконечно длинные отрезки натурального ряда, на которых простых чисел нет вообще (так, среди последовательных чисел x + 2, x + 3, x + 4, …, x + k, где x = 1 ċ 2 ċ … ċ (k – 1) ċ k, нет ни одного простого).

Обозначим через π (n) число простых чисел, меньших n. Немецкий математик Леонард Эйлер доказал, что отношение π (n)n при больших n сколько угодно близко приближается к нулю. Позже математики доказали, что для больших n число π (n)≈nlnn (с понятием логарифма мы познакомимся позже). Также доказано, что для натурального числа n в промежутке [n; 2n] всегда найдется хотя бы одно простое число.

Одно дело – знать, что простых чисел бесконечно много, и совсем другое – доказать, что данное число n является простым. В 2005 году было доказано, что число (2^30402457– 1) простое; оно содержит в своей записи более 900 тысяч цифр.

Определить, является ли большое число простым, очень непросто. В настоящее время эта проблема решается при помощи ЭВМ, однако даже на самых быстрых из современных ЭВМ доказательство того, что число, состоящее из нескольких сотен цифр, является простым, может занять месяцы и годы. На сложности определения простоты чисел основаны современные механизмы шифрования данных.

Справедлива фундаментальная теорема о разложении числа на простые множители.

Любое натуральное число, отличное от 1, единственным образом разлагается в произведение простых чисел с точностью до порядка сомножителей.

Если требуется разложить небольшое число на простые множители, то эти простые множители можно угадать. Для того, чтобы разложить большое число на простые множители, используют следующий приём. Применяют признаки делимости и запись в столбик, причём делимое располагается слева от вертикальной черты, а делители – справа. Разложение на простые множители

Разложить на простые множители число 92820.

Воспользуемся записью в столбик.